Heat Transfer thru Walls and Windows

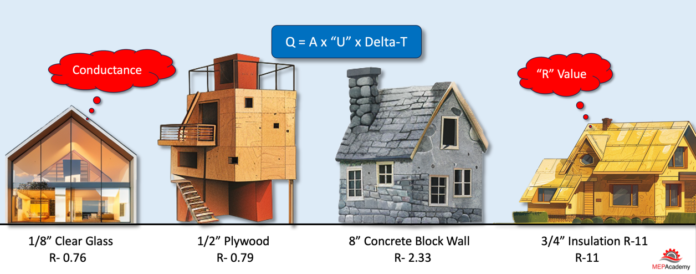
How does the “R” value of a material affect the cooling or heating load of a building? What is the basic equation for the conduction of heat through building construction such as walls and windows? What happens to the total heat when the temperature difference between the outdoors and indoors increases, or the “R” value is doubled?

If you prefer to watch the Video of this presentation, then scroll to the bottom.

We’re often asked to add air conditioning to a space that has never had air conditioning before. One of the factors that needs to be considered is the components of the building shell that will contain the conditioned air. This would be the walls, windows, roof and floors over unconditioned spaces,. 

Here is the equation for the transmission of heat through building components by conductance. This doesn’t consider other heat gain or loss methods, such as infiltration, ventilation, lights, people, plug, or solar loads. This also just looks at single components and not the full wall assembly including interior and exterior air films.

Q = A x U x Delta-T

Where:

Q = Total Btu/Hr.

A = Area (Ft2) of wall or window

U = Building assemblies overall heat transfer coefficient (Btu/hr.ft2.°F)

Delta-T = Difference in outside and inside design temperatures. (°F)

Heat Transfer Examples

Here are a couple of examples of how different construction materials stand up against preventing heat transfer by conductance. This could either be heat coming into the building, or heat going out of the building.

We’ll start with a wall that has 1,000 square feet, and a design indoor temperature of 75 F and an outside design temperature of 90 F. This equates to a 15-degree F delta-T. 

So far, we have the area of the wall and the delta T, the missing factor is the “U” value which is determined by adding up all the resistance of the components of the wall and taking the inverse value.

Here are four different building construction components and their “R” values.

1/8” Clear Glass R=0.76

1/2” Plywood (Douglas Fir) R=0.79

8” Light Weight Concrete Block “R” value = 2.33

3-1/2 R-11 Insulation “R” value =11

We performed the heat transfer equation on each of these building components. Starting with the 1/8” clear glass and an “U” value of 1.32, we get the following.

1,000 Ft2 of Glass x 1.32 “U” Factor x 15 F Delta-T = 19,800 Btu/Hr, or 1.65 Tons of cooling required for the heat gain through conductance. Obviously there glass windows with much better “U” values, but our purpose is to show you how the “R” value and inversely the “U” value effects heat transfer.

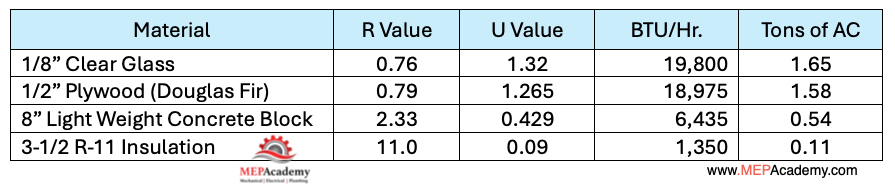
As, you can see if we built the wall with just plywood, we would do a little better with a heat gain of 18,975 Btu/Hr, or 1.58 tons. Using 8” Light Weight Concrete blocks helps considerably by reducing our total heat load in thirds. The greatest effect comes when we add R-11 Insulation to the wall, which in this case looks like this.

1,000 Ft2 of R-11 Insulated wall x 0.09 “U” Factor x 15 F Delta-T = 1,350 Btu/Hr, or 0.11 Tons of cooling. This is a huge reduction in the amount of heat that can transfer from outdoors to indoors. This shows the importance of properly insulating the shell of a building.

This chart shows that the greater the “R” value or resistance of the construction component, the smaller the “U” value will be. The smaller the “U” value, the smaller the heat transfer rate. This is why energy codes mandate a certain “R” value for insulation in walls and roofs.

If the outdoor temperature increased to 105 F, this would double the Delta-T in our equation, which would double the heat gain through our building components. This is one of the reasons why the temperature outdoors makes a difference in the energy consumption of the building for comfort cooling or heating.

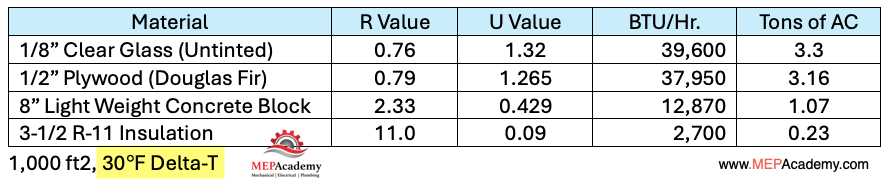
Most energy codes have standard requirements for the total allowable transmission factor that can be used to construct a wall or roof for a space that is air conditioned. It wouldn’t make sense to allow the heating or cooling of a space built with paper walls, as heat would easily enter or escape the space, requiring enormous amounts of energy to condition. 

A high quality wall, floor, window or roof assembly is essential to prevent heat gain or loss in buildings, ensuring energy efficiency and maintaining a comfortable indoor environment by effectively insulating against external temperature fluctuations. 

1/8” Clear Glass R=0.76

Solve for U Value. U = 1/R

• U = 1/0.76 = 1.32
• Q = A x U x Delta-T
• Q = 1,000 ft2 x 1.32 x 25 Delta-T
• Q = 33,000 Btu/hr.

1/2” Plywood (Douglas Fir) R=0.79

Solve for U Value. U = 1/R

• U = 1/0.79 = 1.265
• Q = A x U x Delta-T
• Q = 1,000 ft2 x 1.265 x 25 Delta-T
• Q = 31,625 Btu/hr.

8” Light Weight Concrete Block R=2.33

Solve for U Value. U = 1/R

3-1/2 R-11 Insulation R=11

Solve for U Value. U = 1/R

• U = 1/11 = 0.09
• Q = A x U x Delta-T
• Q = 1,000 ft2 x 0.09 x 25 Delta-T
• Q = 2,250 Btu/hr.